Find The Volume Of A Sphere With A Diameter Of 6 Centimeters

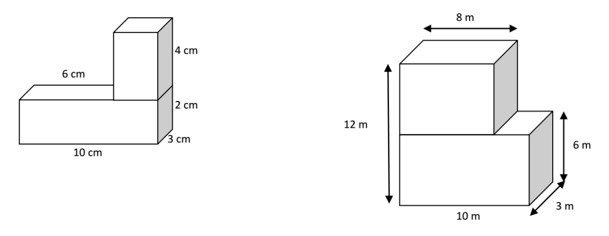
A simple check on any formula for area or volume is a dimensional check. Area is the two-dimensional amount of space that an object occupies. Area is measured along the surface of an object and has dimensions of length squared; for example, square feet of material, or square centimeters. Volume is the three-dimensional amount of space that an object occupies. Volume has dimensions of length cubed; for example, cubic feet of material, or cubic centimeters (cc's). Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities.

Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids. These solids differ from prisms in that they do not have uniform cross sections. Learn about the three-dimensional shapes called cylinders.

Discover the characteristics of cylinders and how to calculate the volume and surface area of a cylinder. Finally, explore using formulas for volume and surface area with practice examples. A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cn and its height is 180 cm.

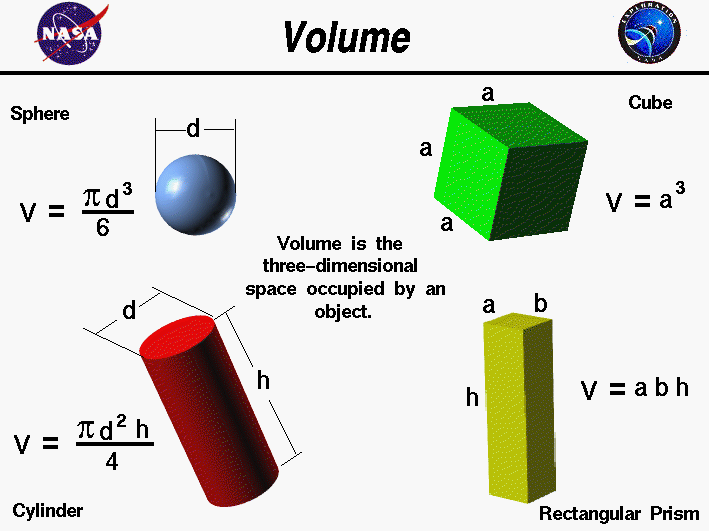
Calculating volume is just another way of saying that you're measuring the amount of space inside a three-dimensional object. You can use standardized formulas for calculating the volume of shapes like cubes, cylinders and spheres, as long as you know their basic measurements. One can calculate theweightof any object by multiplying thedensityof the material by the volume of the object. On this slide, we list some equations for computing the volume of objects which often occur in aerospace. There are similar equations for computing theareaof objects.

The equations to compute area and volume are used every day by design engineers. The volume of sphere is the capacity it has. The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc. The shape of the sphere is round and three-dimensional.

It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume. A glass dome for a lighting fixture is in the shape of a hemisphere. The circumference of the great circle of the hemisphere is 12π inches. Which statements about the hemisphere are true?

Volume Of A Sphere With Diameter Of 6 The total surface area is 108π square inches. The total surface area is 144π square inches. The total surface area is 432π square inches. The total surface area is 36π square inches.

This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C. It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . The following video shows how to solve problems involving the formulas for the surface area and volume of spheres.

For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume.

The volume of a sphere formula can be found in terms of the diameter. The diameter of a sphere is the longest line that is inside the sphere and that passes through the center of the sphere. A sphere is a three-dimensional shape that is perfectly symmetrical and round in shape. Some examples of spheres are a ball, a globe, etc. The volume of a sphere is the amount of space that is inside it the capacity of the sphere that it can hold.

In this article, we will derive the diameter of a sphere formula using the volume. If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r. The radius is 3/2 inches, so I double that to find the diameter. The diameter of the ball is 3 inches, which is greater than the allowed range of diameters.

Given radius of sphere, calculate the volume and surface area of sphere. Q.9.A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as show in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article. Learn the formula for the volume of cylinders, cones and spheres, and the terms used in the formula. Learn the method to find the volume of each shape, with examples.

In geometry, a cylinder is a three-dimensional shape with a circular base, a circular top and straight sides. It is the solid figure that you get when you rotate a rectangle about one of its sides. In most cases when we talk about the volume of a cylinder, we are talking about how much liquid it can hold. Q.1.A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π. Q.5.A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube.

Determine the surface area of the remaining solid. The following figure gives the formula for the volume of sphere. Scroll down the page for examples and solutions.

A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere. A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other.

A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent. Learn about a hemisphere shape and the hemisphere definition in geometry.

Discover the properties of hemispheres and the formulas to calculate those properties. A regulation baseball must have a diameter between 2.87 and 2.94 inches. The surface area of a particular baseball is 9π square inches. Is the baseball within the range of regulation size?

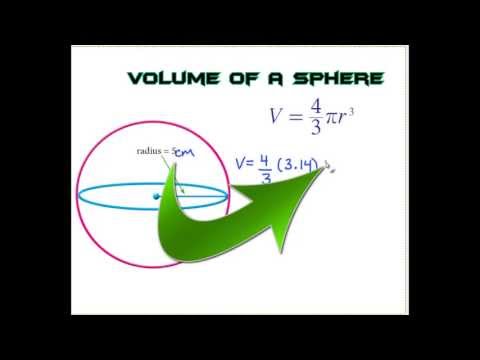
This distance r is the radius of the sphere, and the given point is the center of the sphere. The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. A vessel is in the form of an inverted cone.

Its height is 8 cm and the radius of its top which is open is 5 cm. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel. A sphere of diameter 6 cm is dropped into a cylindrical vessel partly filled with water.

If the sphere is completely submerged in water, find by how much the surface level of water will be raised. Q.6.Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained. Q.5.A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm.

When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-forth of the water flows out. Q.2.A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. Try the free Mathway calculator and problem solver below to practice various math topics.

Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts. Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems. The water level in a cylindrical container of radius 0.5 m is 3.2 m.

When a spherical solid object is completely submerged in the water, the water level rises by 0.6 m. The sphere is an extended version of a circle. Or it will be right to say a 3D version of a circle. In geometry, a sphere is a 3-dimensional round solid figure in which every point on its surface is equidistant from its center. Archimedes' principle helps us find the volume of a spherical object.

It states that when a solid object is engaged in a container filled with water, the volume of the solid object can be obtained. Because the volume of water that flows from the container is equal to the volume of the spherical object. In mathematics, area is defined as the amount of space taken up by a two-dimensional figure. Learn about the definition of area and how to use a formula to calculate the area of uncommon shapes. A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters.

Round the answer to the nearest hundredth. Find the baseball's volume in cubic centimeters. Q.1.A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.

Q.6.A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig.). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Q.3.A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. Take a hemisphere of radius and look at the area of a typical cross-section at height above the base. Thus the development of volume formulas are important for students, as is the careful memorizing of the key formulas, such as the volume of a sphere.

We can then integrate this to obtain the total volume. This method can be used very effectively to find the volume of solids which do not have uniform cross-section, and may have curved boundaries. Many sports that are played with the help of the ball require studying the sphere, as well as its properties. For example, in football, the surface area and volume of a ball is of extreme importance.

Different volumes and surface areas of a ball can affect to speed of the kick, trajectory of the ball and its swing in the air. Apart from football, the surface area and volume of a sphere is important in many other sports as well. Tennis, handball, baseball, golf, basketball all these sports are revolving around the spherical balls. Any cross section of a sphere by a plane is a circle.

The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres. A spherical solid metal of a radius of $16$ inches is melted down into a cube. What will be the dimensions of the cube? Use $\pi \approx 3.14$ and estimate your answer to the nearest whole number.